I was solving some HackerRank problem the other day and to get 100% it required to use priority queue. I don’t remember the exact task and can’t find it neither, but in each iteration you had to pick the lowest number from an array. This array was being modified all the time, so it was not possible to just sort it once and take consecutive items. It required a data structure allowing for fast retrieval of min or max value.
Ruby does not have built-in priority queue implementation or at least I was not aware of one. There are gems, but again you can’t use them in HackerRank. I had to implement my own and I think it is good to know how to do it.
In this article I will explain what is a binary heap and how can it be used to implement a priority queue in Ruby.
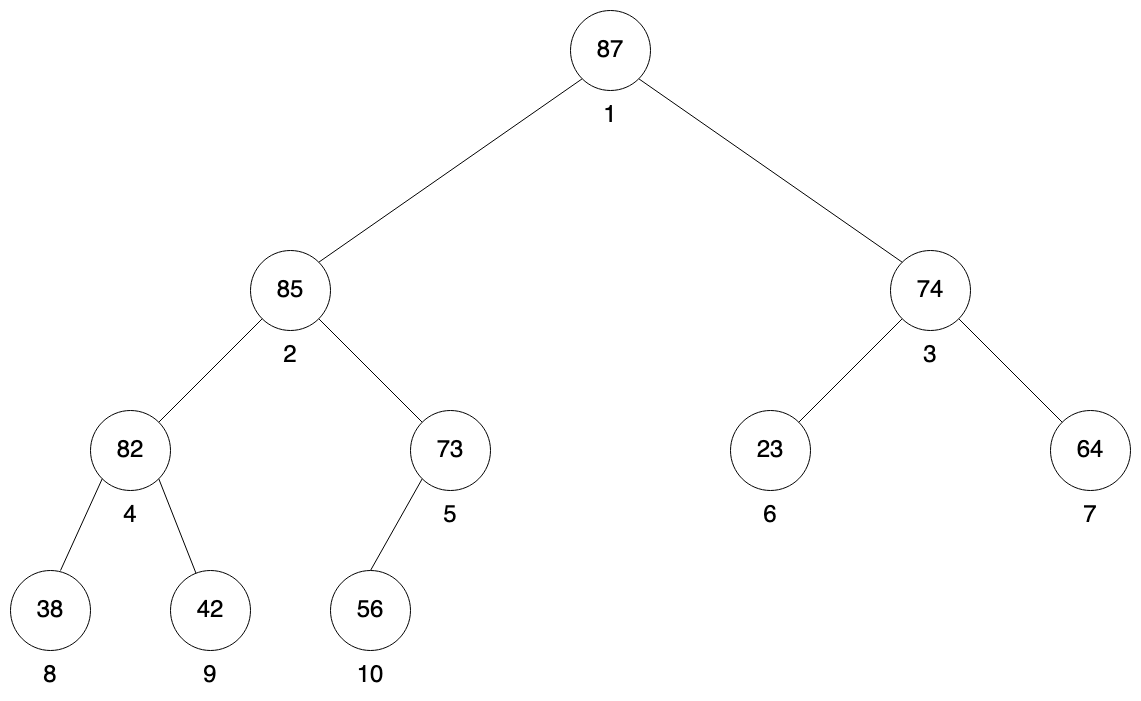
Binary heap is generally a binary tree with specific properties. Binary means that each node can have at most 2 child nodes. Special thing about heaps is that all leaf nodes (nodes without children) are aligned to the left. Nodes are numbered top to bottom, left to right starting from 1. See the figure below.

Using such numbering allows to quickly calculate indexes for parent node as well as left and right child. If X is the index of current node then parent index is X / 2, left child index is X * 2 and right child index is X * 2 + 1.
The main heap property says that parent node must be greater or equal than its children. Such heap is then called max heap. We can change this condition to less or equal and then we it will be called min heap. For now we will focus on max heaps.
Let’s start our Ruby implementation with helper methods for calculating parent, left and right children.
class Heap
private
def parent(x)
x / 2
end
def left(x)
x * 2
end
def right(x)
x * 2 + 1
end
end
Heap property means that parent node must be greater or equal than its children. Or that node cannot be greater than its parent. When operating on a heap in certain situations this heap property can be violated and it will need to be restored. We are only considering situations when one node is out of place. The left sub-tree is proper heap, right child is proper heap, but the value in node can be less than left or right node. To fix such violation, this rebelious node must bubble down to the correct place.
The procedure for fixing heap property is considering values of current node and its children. It starts with finding which of these nodes has the largest value. If the current node has the largest value the heap property is already preserved and there is nothing more to do. If however left or right child is larger, then current node is swapped with the larger node and procedure is executed again on the lower node. Procedure is stopped when the problematic node is in the correct place and heap property is preserved. When bubbling down left node is always considered first. Remember that nodes must be aligned to the left.
Before we go into implementation of this procedure, let’s first add a couple more methods to our class:
class Heap
def initialize(array)
@data = array
@size = array.size
end
private
def get(x)
@data[x - 1]
end
def swap(x, y)
@data[x - 1], @data[y - 1] = @data[y - 1], @data[x - 1]
end
# rest of the class
end
Heaps are usually implement with arrays and our constructor will accept any array that will be converted into a heap. Additional @size variable is required, because heap can have less items than will be present in this array. In case of removing items from heap, the heap size will decrease, but those items will be still present in the array. They will be placed at indexes greater than heap size.
Heap nodes are indexed starting from 1, because it allows quick calculations of parent, left and right child indexes. But Ruby arrays are indexed from 0. It is possible to adjust calculations in every place we are dealing with indexes (parent, left, right methods and so on), but in my opinion it is much easier to just have it in one or two places.
Implementation presented in this article is using indexes from 1, but for accessing actual elements in the array we will use dedicated methods that will subtract one from the index. Like get and swap methods above. Get just returns the value at given index and swap swaps values at given indexes.
And here is method to maintain heap property:
class Heap
# rest of the class
def heapify(x)
return if @size < x
l = left(x)
r = right(x)
largest = x
if l <= @size && get(l) > get(x)
largest = l
end
if r <= @size && get(r) > get(largest)
largest = r
end
if largest != x
swap(x, largest)
heapify(largest)
end
end
private
# rest of the class
end
It checks if left or right child is larger than current node and assign index of largest node to largest variable. If current node is not the largest one, it swaps it with the largest one. And then it is called again on the index that was the largest.
Let’s visualize how this method works. We will use the heap from the example above, but with value changed at root from 87 to 18.
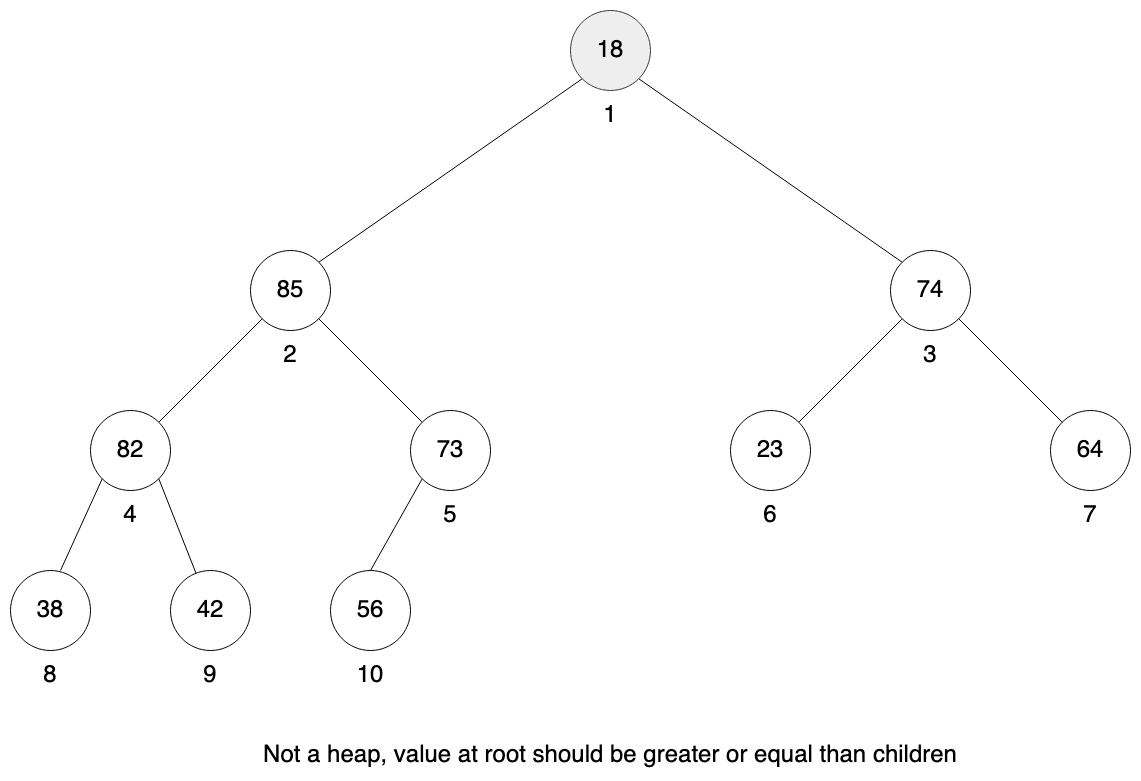
It is not a valid heap anymore, because root node does not have heap property. It’s both children are greater than parent. But if you look at both children and their sub-trees, you can see those are actually valid heaps. It is required for heapify method to work.
To fix heap property we need to consider both children and pick which one is larger, starting from the left. Left child is 85 and right child is 74, so we choose 85 and swap node 1 with node 2.
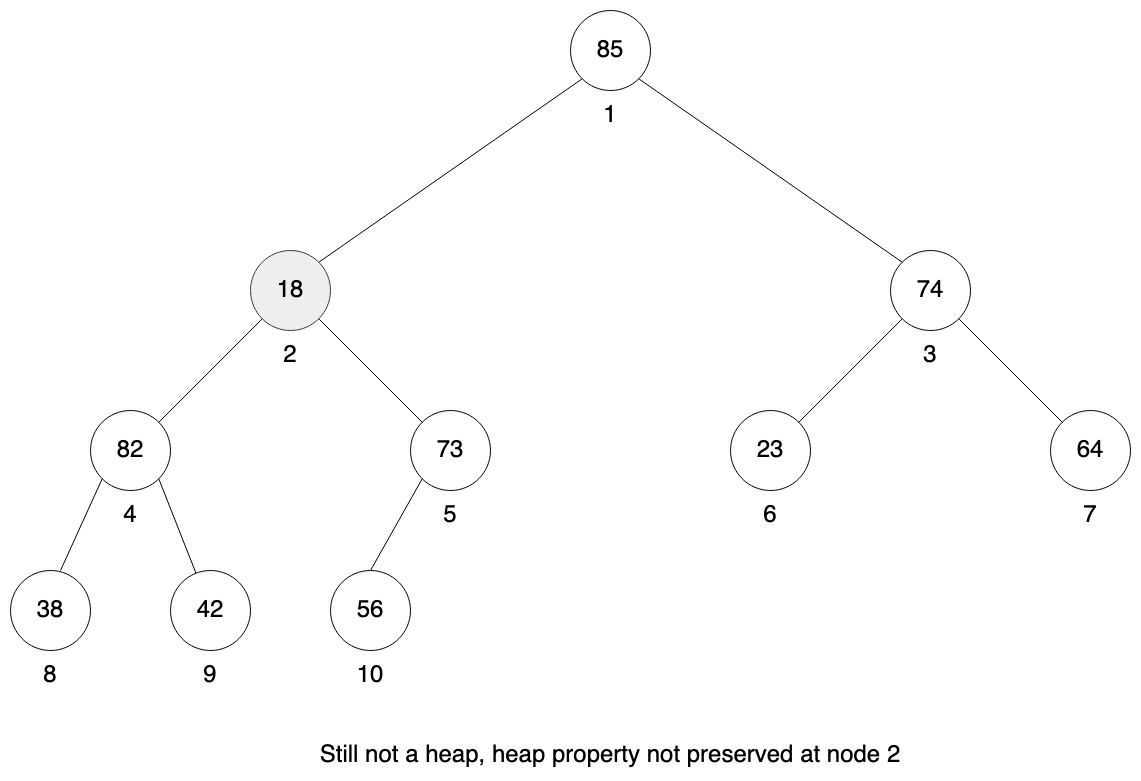
Now we repeat this process for node 2. Left child is 82, right child is 73, so we choose 82 and swap node 2 with node 4.
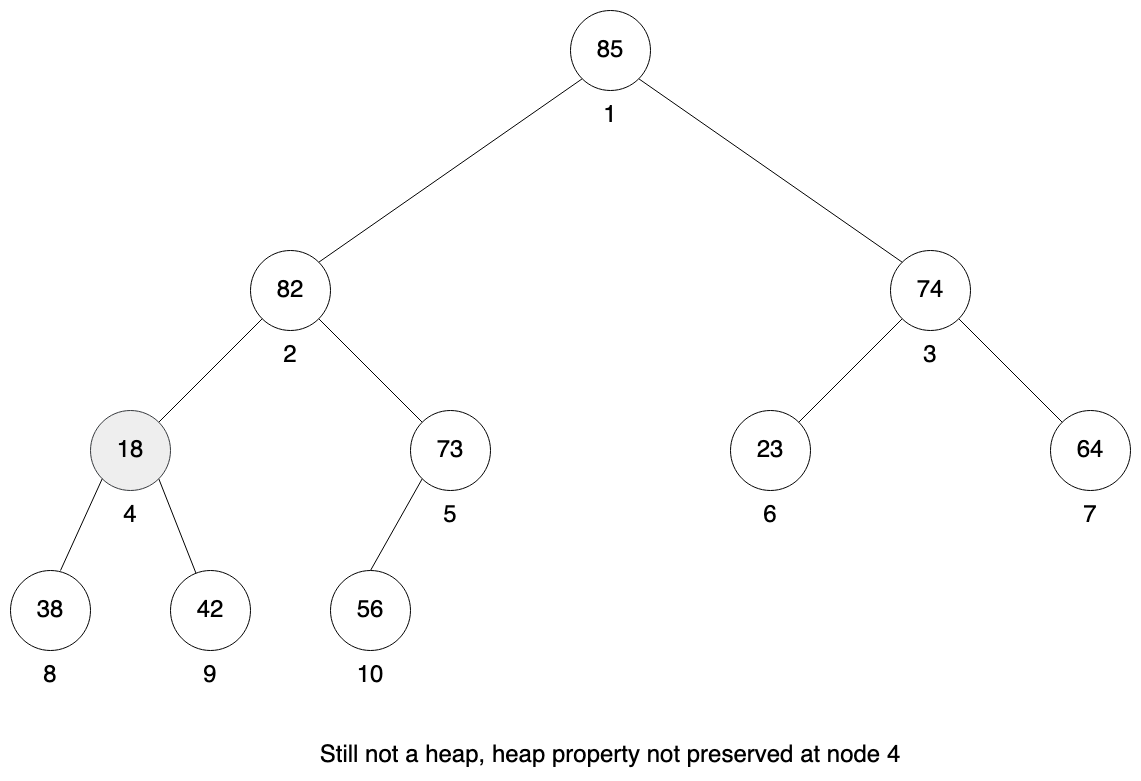
We repeat the process for node 4. You can see that heap property is not preserved there. We check our left child which is 38 and our right child is 42. Right is larger so we swap node 4 with node 9.
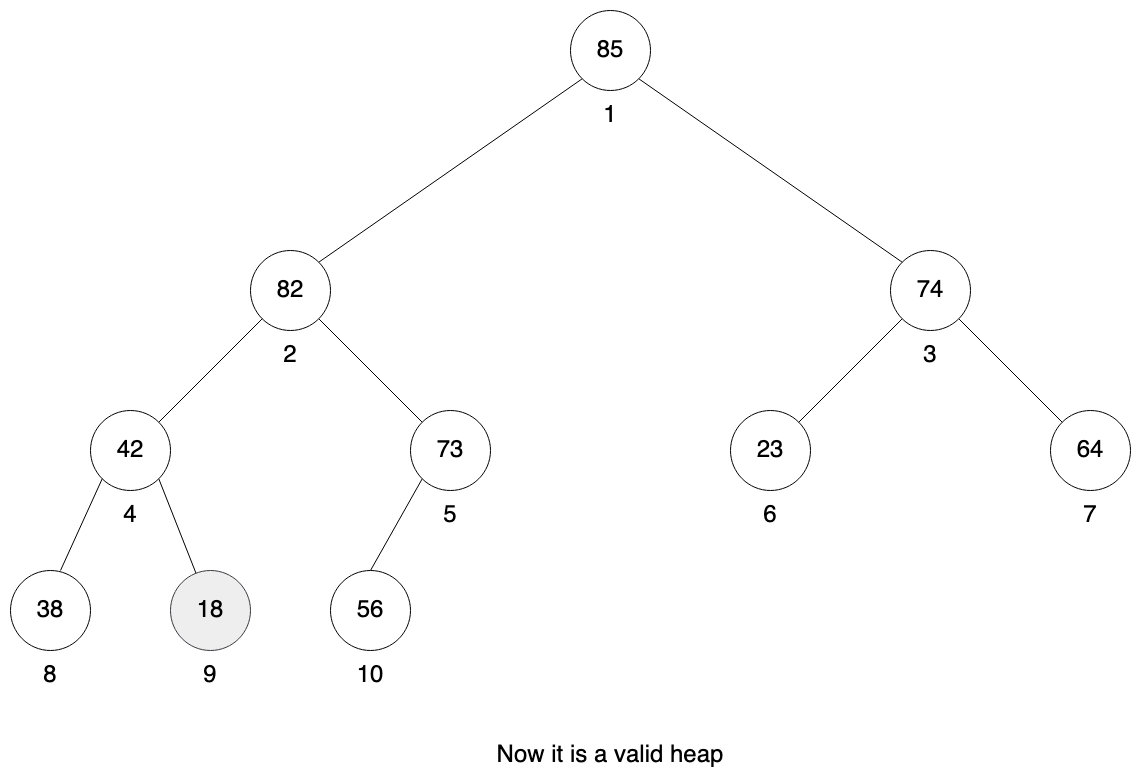
We are in the leaf node so the method stops and we have a valid heap as a result.
Heapify method can be used to build heap from initial array. Looking at the figures above we can see that half of heap nodes are actually leaves. And they are all placed in the second half of our array. When looking at just one leaf node we can consider it a proper heap of size 1.
But the first half of our array have elements that may violate the heap property, so it needs to be fixed. Heapify method requires that both left and right children are proper heaps. We can start executing heapify method on the first parent node of two leaves. This will be the middle element of our array and then we can move left to the beginning of the array. After that we will have proper heap.
Here is the implementation of building the heap:
class Heap
# rest of the class
def initialize(array)
@data = array
@size = array.size
build
end
def build
(@size / 2).downto(1) do |x|
heapify(x)
end
end
def to_a
@data
end
private
# rest of the class
end
I think it makes sense to build heap straightaway from the initial array in the constructor. to_a method can be useful to see how the heap looks like.
# create array with 10 random numbers
array = Array.new(10) { rand(100) }
puts array.inspect
# create heap from that array
heap = Heap.new(array)
puts heap.to_a.inspect
# output
[56, 87, 74, 42, 73, 23, 64, 38, 82, 85]
[87, 85, 74, 82, 73, 23, 64, 38, 42, 56]
Let’s visualize this using input array [56, 87, 74, 42, 73, 23, 64, 38, 82, 85]. This array has 10 elements and we need to start in the middle to get our first non-leaf element. Please note that if this array would have 11 elements, we would still start at 11 / 2 = 5, node 5.
The sub-tree at node 5 is not a valid heap, the largest element has value 85 in the left child. We need to swap node 5 with node 10.
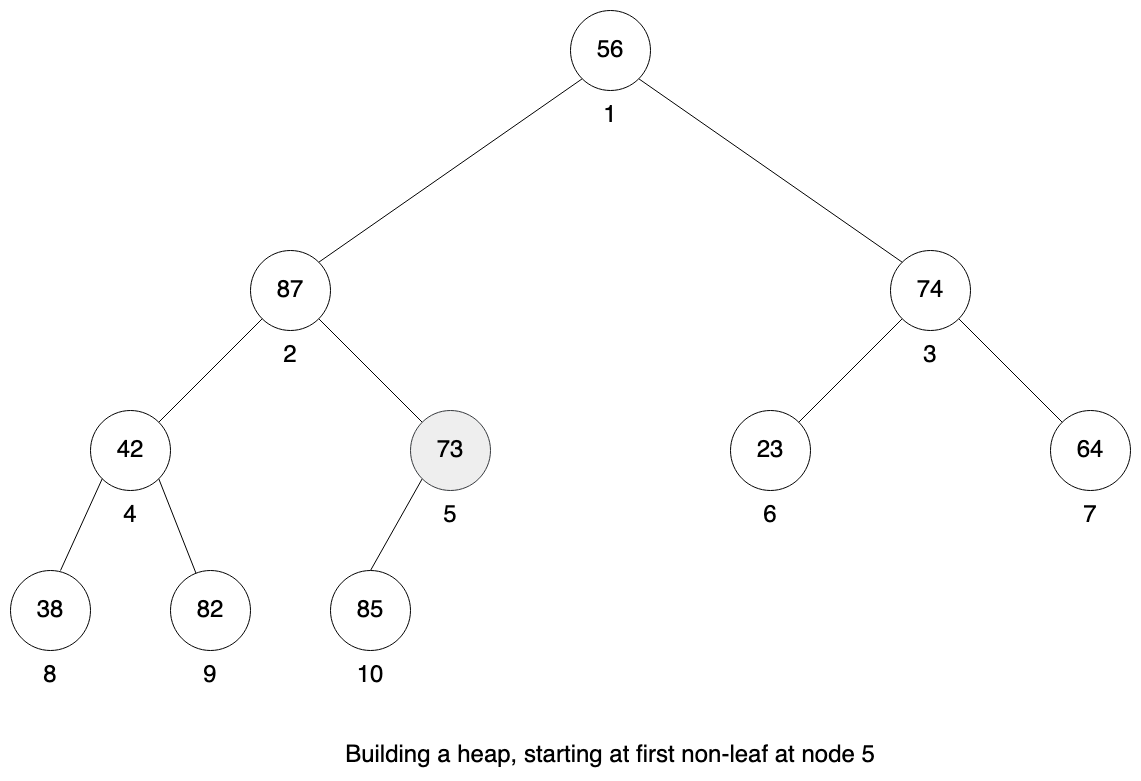
Now the sub-tree at node 5 is a valid heap. We repeat the process for the next non-leaf node 4. Here again is not a valid heap as the largest value is at the right child. We need to swap node 4 with node 9.
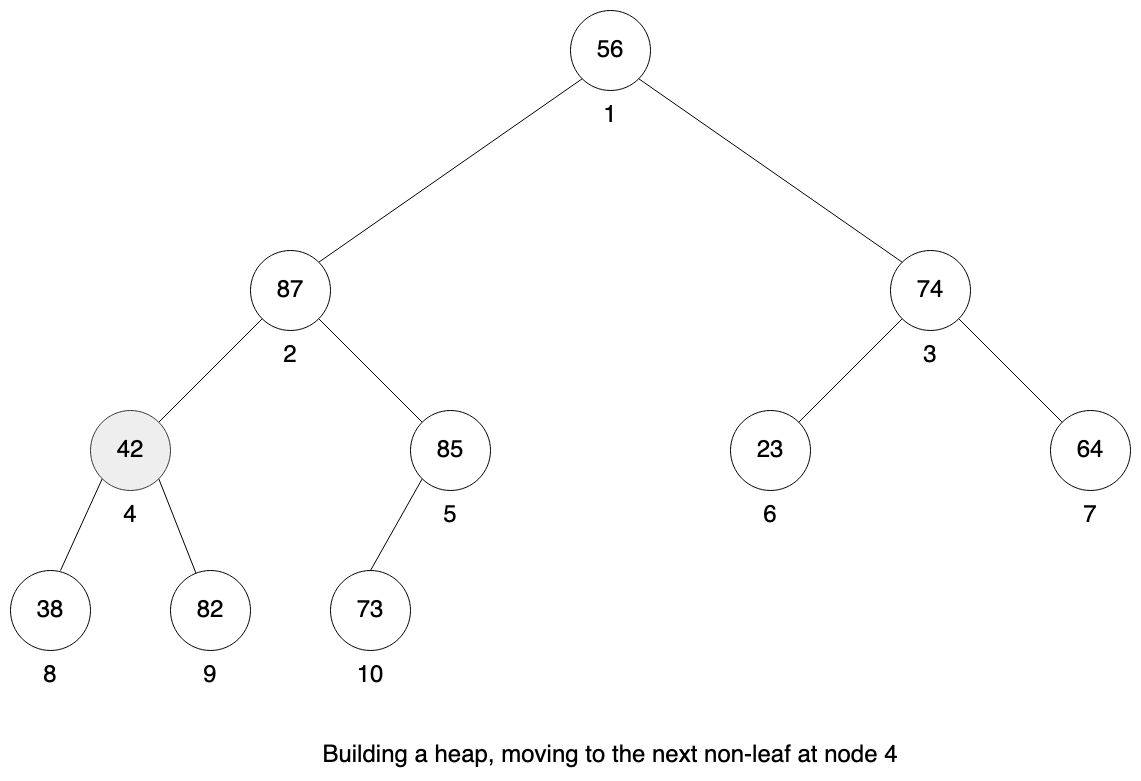
Sub-tree at node 4 is a valid heap and we continue with next non-leaf node 3.
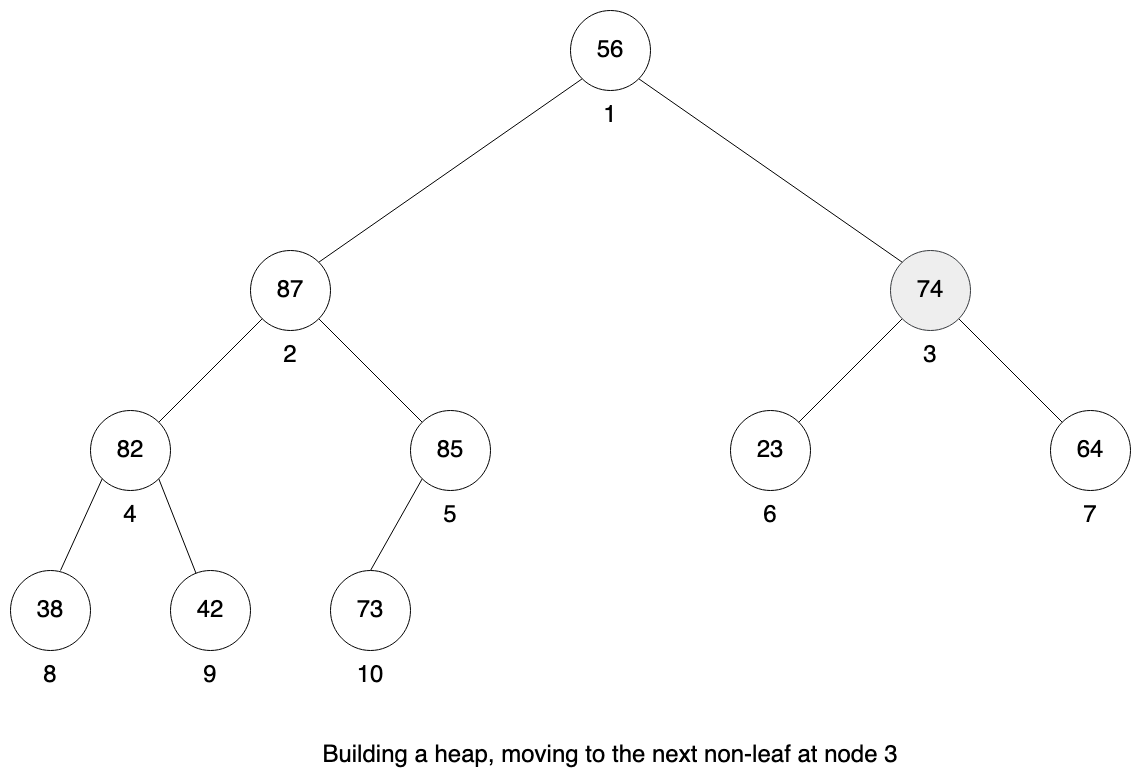
Here everything is fine. It is a valid heap, so no need to do anything.
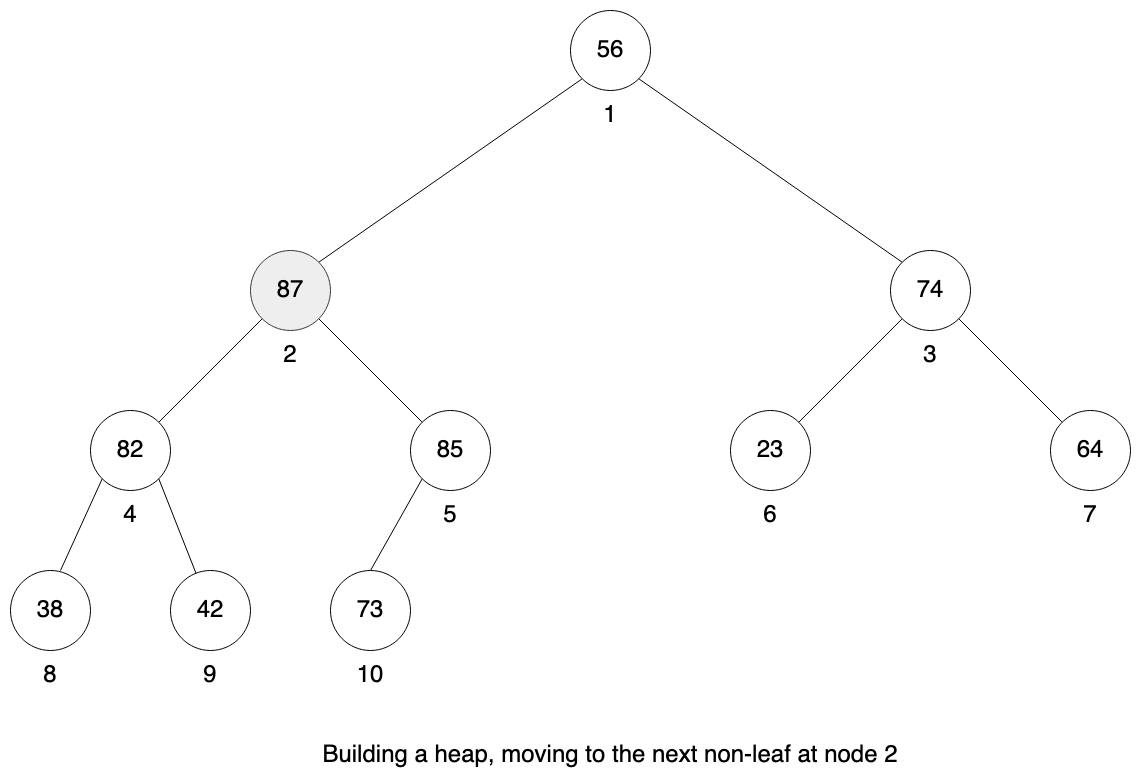
We continue to node 2. This sub-tree is also a valid heap, so no need to do anything.
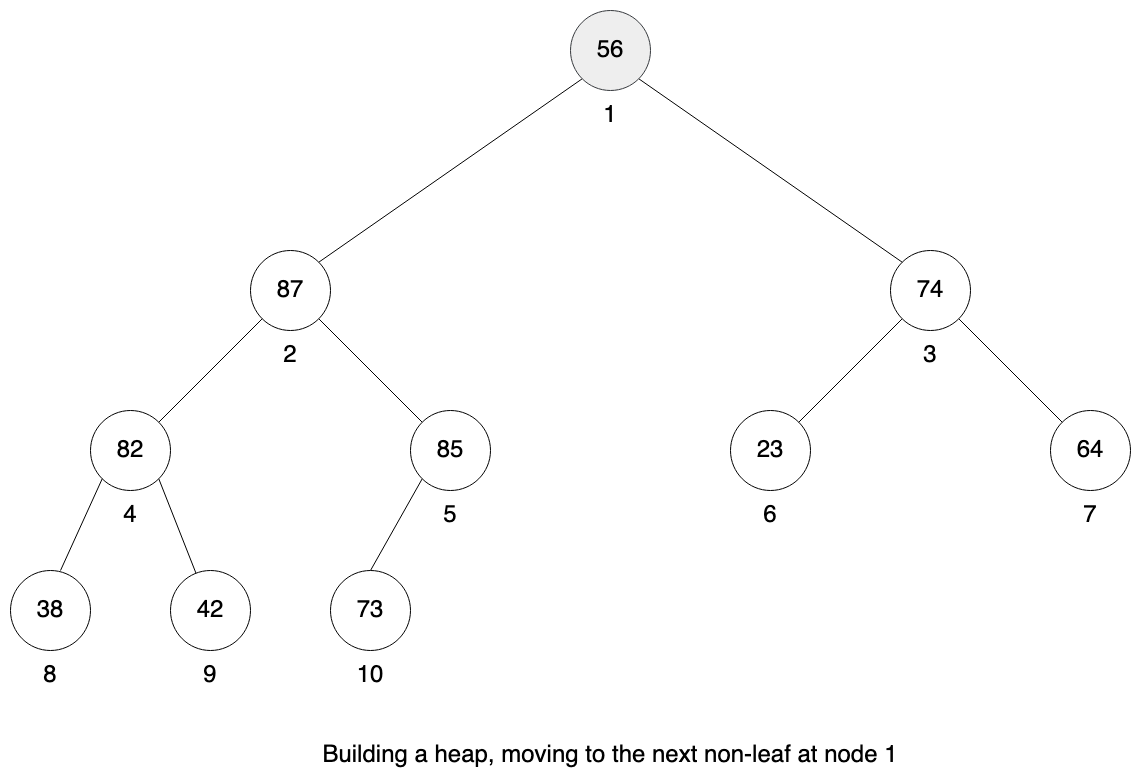
Finally we are at the root and it is not a valid heap. And this time we will need to do more swaps to fix it. We need to bubble down node 1 with value 56 to the correct place. We first need to swap node 1 with node 2, then node 2 with node 5 and finally node 5 with node 10. I didn’t draw all those steps on the figure, because heapify method was already explained earlier in the article.
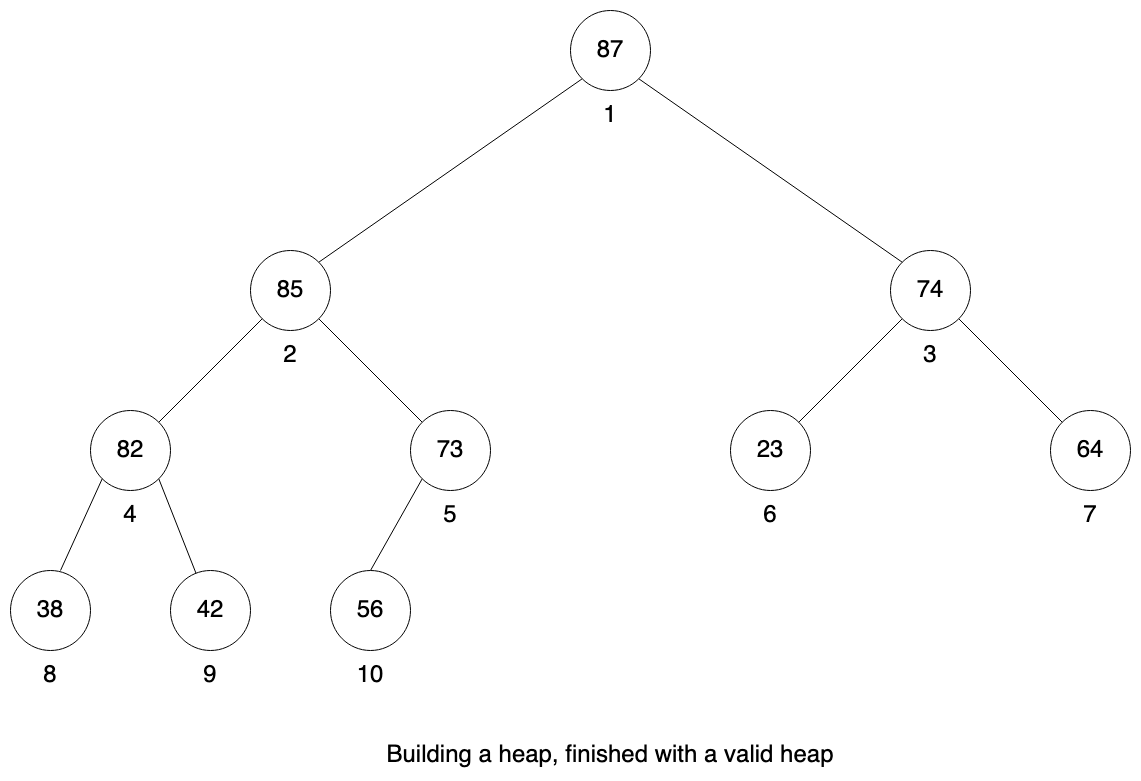
Here is the final result, we have a valid heap.
The priority queue is a data structure containing objects with assigned priority. It allows to add new objects, but the most important operation is extracting the object with max value. And those operations must be fast.
Object with max value is stored at the root of the heap. After removing it, it needs to be replaced with something else and heap property must be preserved. It can be replaced with the last element of the array. Then we can decrease the size of the heap and fix heap property for the root.
class Heap
# rest of the class
def extract
return nil if @size < 1
max = get(1)
swap(1, @size)
@size -= 1
heapify(1)
max
end
def peek
return nil if @size < 1
get(1)
end
# rest of the class
end
In case heap is empty, nil value is returned. Then first element is swapped with the last one, heap size decreased and heap property is fixed for the root element.
Additional peek method can be used to just get the value of max element without removing it from the heap.
The last missing piece is a method to add new elements to the heap. This new element can be added to the end of the array and then it can bubble up to the right place so that heap property is maintained.
class Heap
# rest of the class
def insert(val)
@size += 1
set(@size, val)
i = @size
while i > 1 && get(i) > get(parent(i))
swap(i, parent(i))
i = parent(i)
end
end
private
def set(i, val)
@data[i - 1] = val
end
# rest of the class
end
Let’s visualize inserting new element to our heap / queue. We will start with heap containing the following nodes [87, 73, 74, 42, 56, 23].
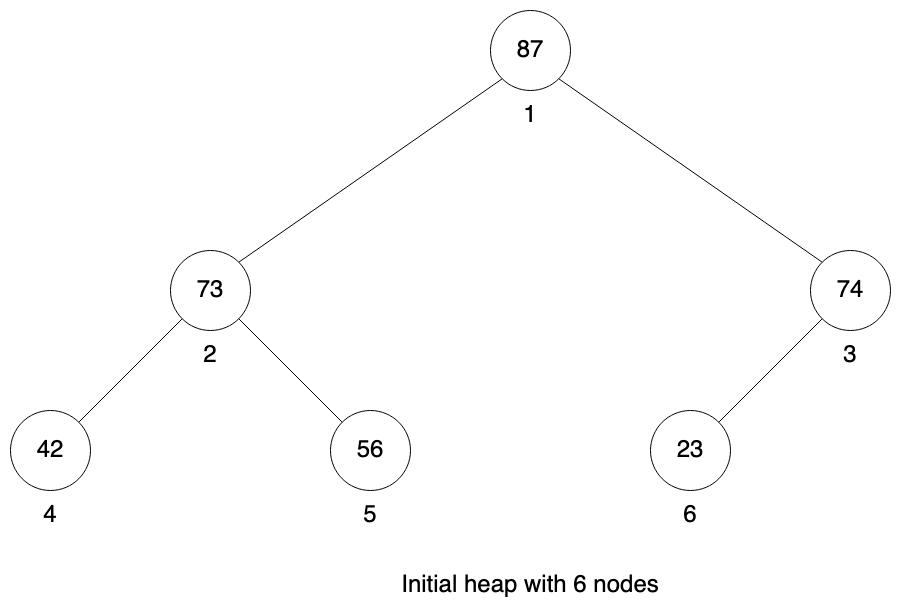
First we increase the size of our heap and insert this new node at the end.
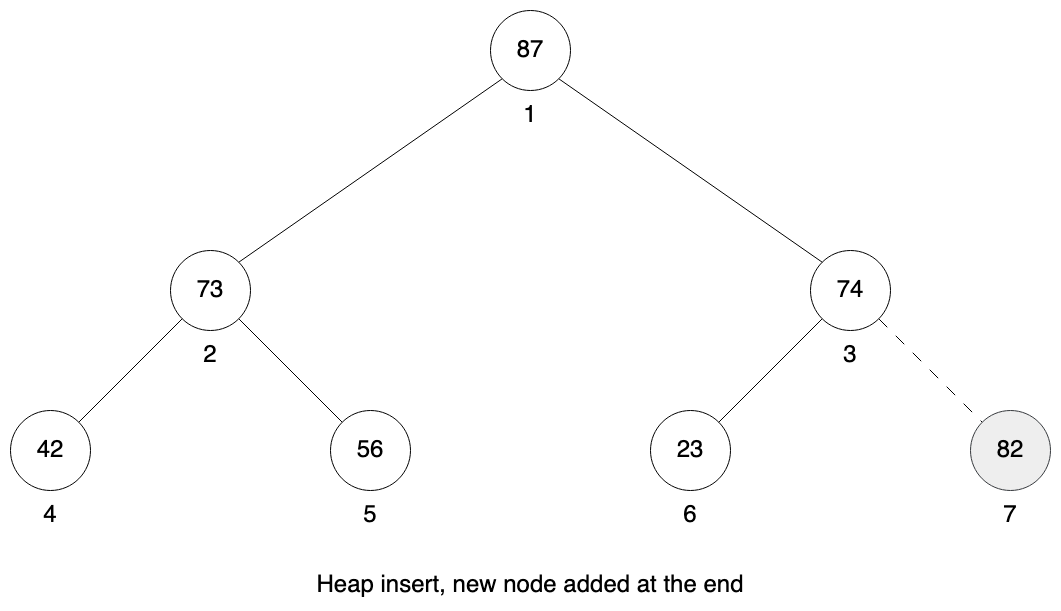
Now until the parent node is smaller we need to swap our current position with our parent. In this case we need to do this just once. 82 is larger than 74, so we swap node 7 and node 3. Then 82 is smaller than 87 in it’s parent so we need to stop.
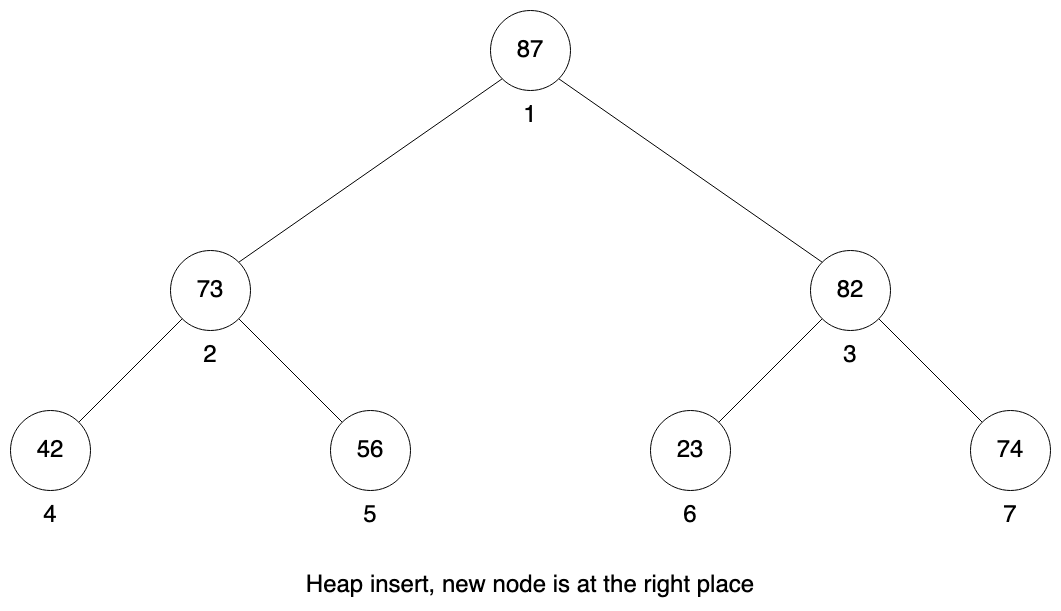
We can also implement method removing element at given index. It works exactly like extracting max element, but it swaps selected index with last element and fixing heap property at selected index.
class Heap
# rest of the class
def delete(x)
return if @size < x
swap(x, @size)
@size -= 1
heapify(x)
nil
end
# rest of the class
end
Our current implementation assumes we are working with array of integers, but in real life we may need to store any arbitrary objects with priority property.
Let’s try to do it with Task class containing description and priority. We will create an array of tasks and then try to create a heap from that array.
class Task
attr_reader :description, :priority
def initialize(description, priority)
@description = description
@priority = priority
end
def inspect
"#{description} (#{priority})"
end
end
tasks = [
Task.new("Do laundry", 10),
Task.new("Make dinner", 20),
Task.new("Pay bills", 100),
Task.new("Just chill", 2),
]
heap = Heap.new(tasks)
puts heap.to_a.inspect
We will get the following error:
heap.rb:15:in `heapify': undefined method `>' for nil:NilClass (NoMethodError)
if l <= @size && @data[l] > @data[x]
^
from heap.rb:34:in `block in initialize'
from heap.rb:34:in `downto'
from heap.rb:34:in `initialize'
from heap.rb:87:in `new'
from heap.rb:87:in `<main>'
There is a problem with comparing two objects. Our code does not know how two compare priority of two different tasks. Fortunately in Ruby there is an elegant way to fix this problem without changing Heap class. We can include Comparable module into Task and implement spaceship (<=>) operator.
class Task
include Comparable
# rest of class
def <=>(other)
priority <=> other.priority
end
# rest of class
end
tasks = [
Task.new("Do laundry", 10),
Task.new("Make dinner", 20),
Task.new("Pay bills", 100),
Task.new("Just chill", 2),
]
heap = Heap.new(tasks)
puts heap.to_a.inspect
# output
[Pay bills (100), Make dinner (20), Do laundry (10), Just chill (2)]
So far we implemented a max heap, where the largest element is at the root. Sometimes we need min heap and it is easy to convert max heap into min heap. We just have two places in code that compare heap elements: heapify and insert methods. Both use greater than comparison. We can introduce heap type variable and in case of min heap we will change this comparison to less than.
class Heap
def self.min(array)
new(:min, array)
end
def self.max(array)
new(:max, array)
end
def initialize(type, array)
@type = type
@data = array
@size = array.size
build
end
def heapify(x)
return if @size < x
l = left(x)
r = right(x)
selected = x
if @type == :max
if l <= @size && get(l) > get(x)
selected = l
end
if r <= @size && get(r) > get(selected)
selected = r
end
else
if l <= @size && get(l) < get(x)
selected = l
end
if r <= @size && get(r) < get(selected)
selected = r
end
end
if selected != x
swap(x, selected)
heapify(selected)
end
end
def insert(val)
@size += 1
set(@size, val)
i = @size
if @type == :max
while i > 1 && get(i) > get(parent(i))
swap(i, parent(i))
i = parent(i)
end
else
while i > 1 && get(i) < get(parent(i))
swap(i, parent(i))
i = parent(i)
end
end
end
# rest of the class
end
It is possible to implement more compact solution. We could use Ruby metaprogramming to have single codebase for both cases. But I think this is more easier to understand and I will keep it like that.
Now we can use it like that:
heap = Heap.min([4, 2, 1, 8, 3])
puts heap.to_a.inspect
heap = Heap.max([4, 2, 1, 8, 3])
puts heap.to_a.inspect
# output
[1, 2, 4, 8, 3]
[8, 4, 1, 2, 3]
Heap can be used for sorting. Because the largest element is always at the root, the sort procedure can swap first element in the array with the last one, then decrease the size of the heap and fix heap property at the root. Now the largest element is at the end of the array and outside of the heap. This is the reason why we need to have separate variable for storing heap size.
We can repeat this procedure until whole array is sorted.
class Heap
# rest of the class
def sort
(@size - 1).times do
swap(1, @size)
@size -= 1
heapify(1)
end
end
# rest of the class
end
array = Array.new(10) { rand(100) }
puts array.inspect
heap = Heap.max(array)
heap.sort
puts heap.to_a.inspect
# output
[84, 44, 22, 9, 87, 17, 96, 87, 25, 11]
[9, 11, 17, 22, 25, 44, 84, 87, 87, 96]
The above sort method is using max heap to sort input array. If we use min heap instead, the array will be also sorted by in descending order.
Let’s visualize this method using input array from above [84, 44, 22, 9, 87, 17, 96, 87, 25, 11]. This is just some random array, we need to start with building heap from that. The first figure shows already valid heap. In each step we will visualize the size of our heap and the size of our array. The array will have constant size of 10 elements, but our heap will decrease by 1 in each step.
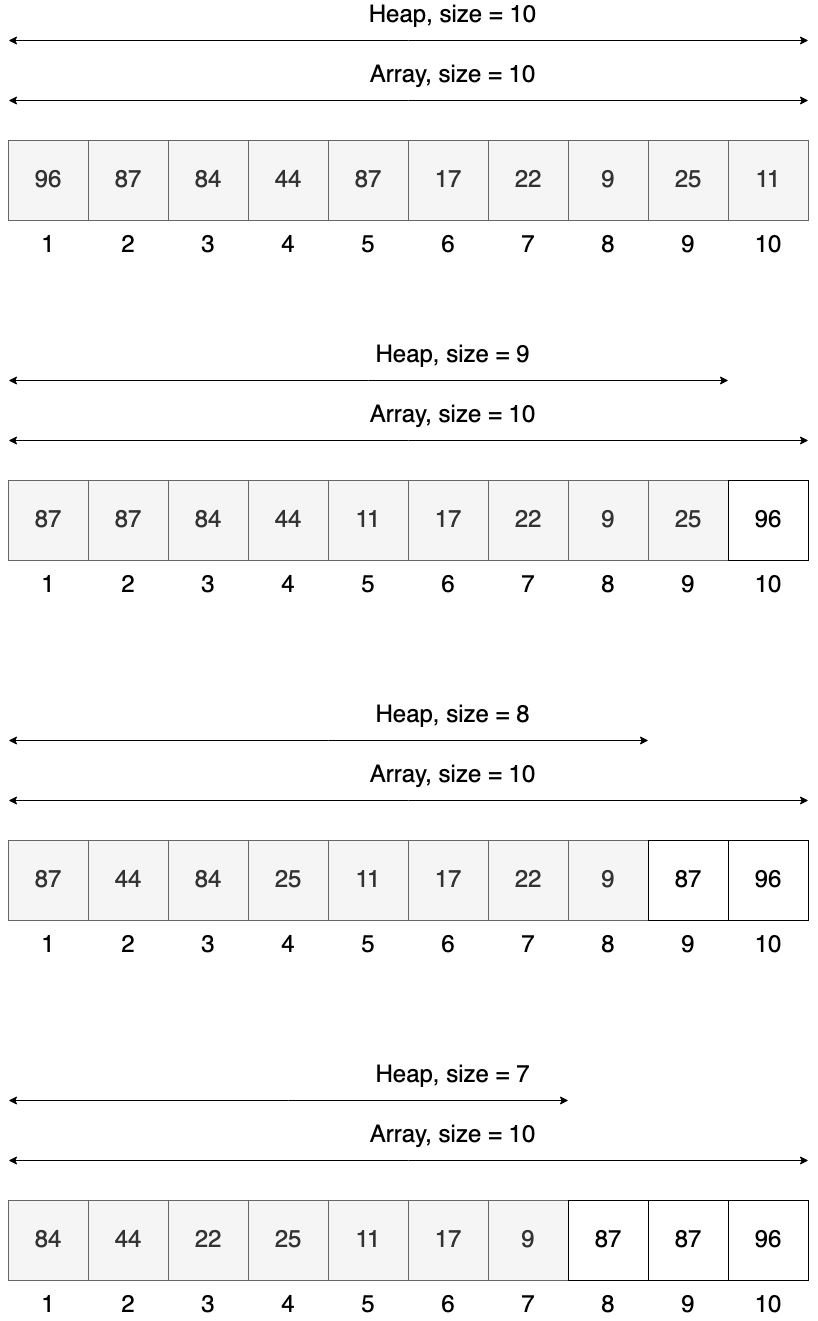
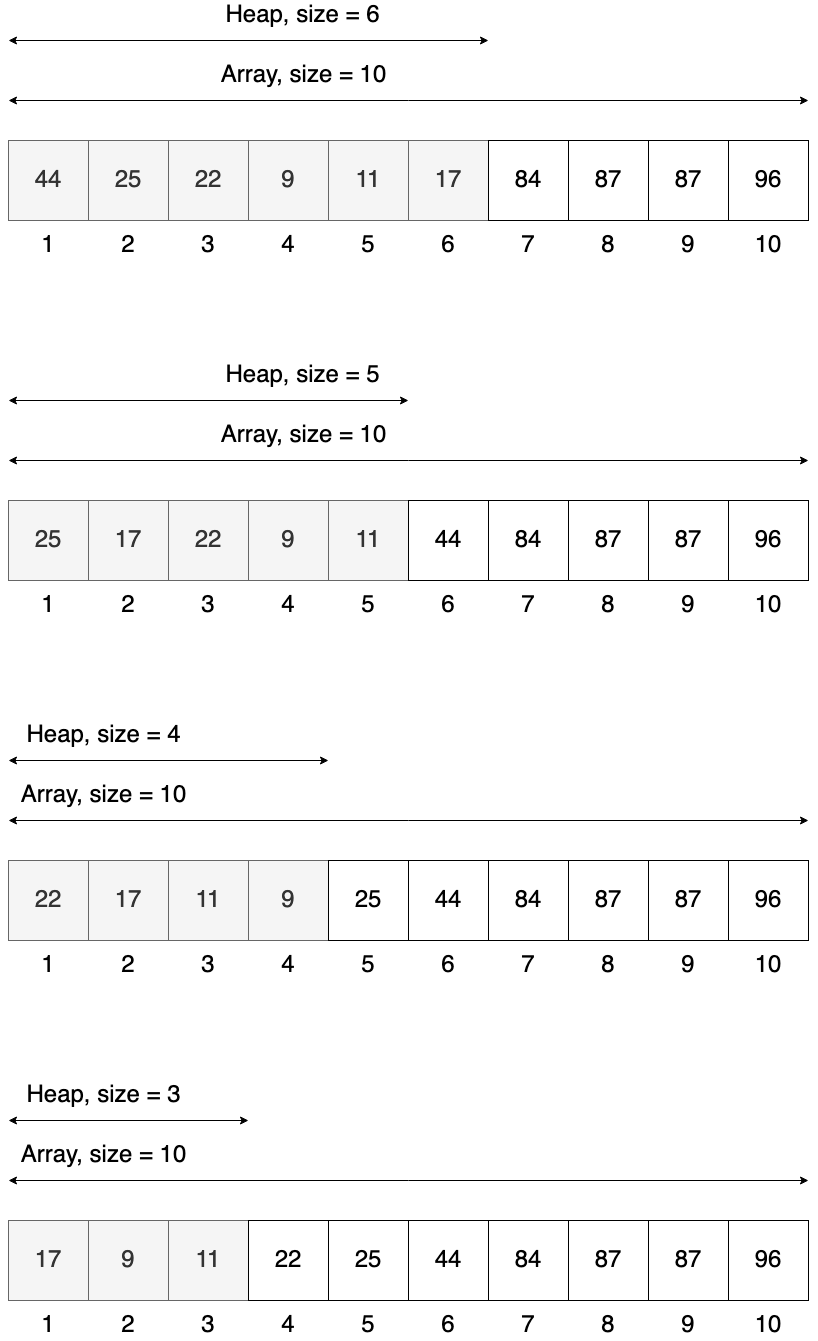
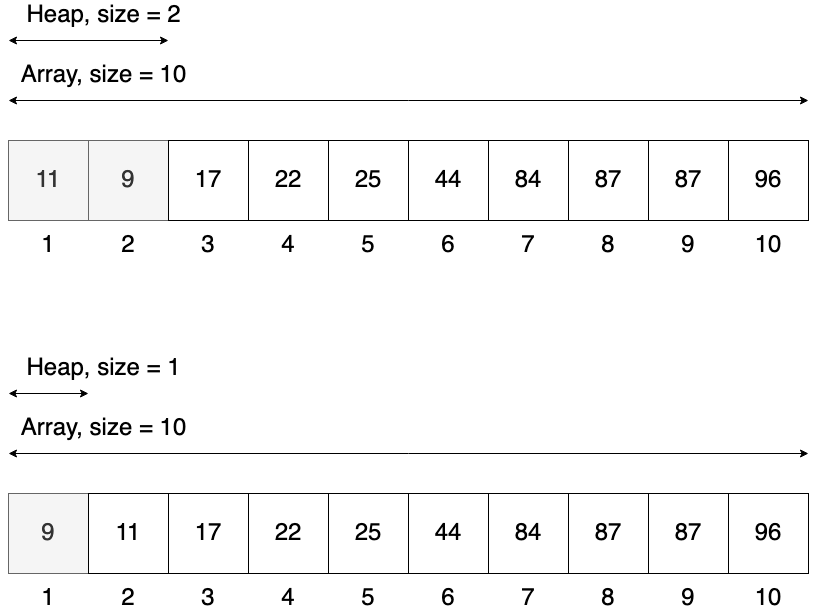
In the end with have all elements sort, but our initial heap is destroyed. This is a problem so I think it is better to have a slightly different interface:
class Heap
# rest of the class
def self.sort(array)
heap = max(array)
heap.send(:sort)
heap.to_a
end
private
def sort
(@size - 1).times do
swap(1, @size)
@size -= 1
heapify(1)
end
end
# rest of the class
end
Now the actual sort method is hidden as an internal api, so clients should not call it directly on the heap. Instead we have class method that gets array as input. This array is converted to heap, sorted and then returned.
Heapsort has certain advantages. It is fast, it is done in place, meaning no additional memory is required. But it is also not stable. This mean when there are elements with the same value in the initial array they may appear in different order in the sorted array. It is not a problem when you are sorting integers, but is important when sorting more complex object.
We can check this for our Task class:
tasks = [
Task.new("Task 1", 1),
Task.new("Task 2", 1)
]
puts Heap.sort(tasks).inspect
# output
[Task 2 (1), Task 1 (1)]
Tasks are now in reverse order. Stable sorting algorithm would return them in the same order as in the input array. This property is crucial if you want to sort arrays multiple times using different attributes. And as I said before it does not matter for plain numbers.
Anyway I read mentions in multiple places that sorting is usual implemented using Quicksort algorithm as it is faster in practice.
In the end it’s worth to mention time complexity of various heap operations. See the table below.
| Operation | Time Complexity |
|---|---|
| Heapify | O(log n) |
| Build | O(n) |
| Extract min / max | O(log n) |
| Peek | O(1) |
| Insert | O(log n) |
| Delete | O(log n) |
| Sort | O(n * log n) |
Heapify is the most important as it is a base for other operations. The number of operations heapify needs to performed is constrained by the height of the tree. And because heap is a balanced tree, the size is log n.
Build operation is performing heapify operation n times, so technically it should be O(n * log n), but it starts on heaps that are smaller than the main heap. First it is called for heaps of size 2, then heaps of size 3 and so on. Please look at the heap below.

5 nodes are leaves so we don’t do anything with them. Then we have heaps of size 2 at nodes 5, 4 and 3, heapify for them will do max 1 operation. Then we have heap of size 3 at node 2, which will take max 2 operations and heap of size 4 at node 1 with max 3 operations. So in the end we can build our heap from initial array in linear time.
Extract and delete operations have the same complexity as heapify O(log n). Insert is also O(log n) as in the worst case the new element needs to bubble up to the root of the heap.
And finally sort is O(n * log n) as we are calling heapify method O(n) times.
Below is the full implementation in Ruby that was used in this article. For sure it can be improved and made more compact, but I decided to leave it like that for simplicity.
class Heap
def self.min(array)
new(:min, array)
end
def self.max(array)
new(:max, array)
end
def initialize(type, array)
@type = type
@data = array
@size = array.size
build
end
def build
(@size / 2).downto(1) do |x|
heapify(x)
end
end
def heapify(x)
return if @size < x
l = left(x)
r = right(x)
selected = x
if @type == :max
if l <= @size && get(l) > get(x)
selected = l
end
if r <= @size && get(r) > get(selected)
selected = r
end
else
if l <= @size && get(l) < get(x)
selected = l
end
if r <= @size && get(r) < get(selected)
selected = r
end
end
if selected != x
swap(x, selected)
heapify(selected)
end
end
def extract
return nil if @size < 1
max = get(1)
swap(1, @size)
@size -= 1
heapify(1)
max
end
def peek
return nil if @size < 1
get(1)
end
def insert(val)
@size += 1
set(@size, val)
i = @size
if @type == :max
while i > 1 && get(i) > get(parent(i))
swap(i, parent(i))
i = parent(i)
end
else
while i > 1 && get(i) < get(parent(i))
swap(i, parent(i))
i = parent(i)
end
end
end
def delete(x)
return if @size < x
swap(x, @size)
@size -= 1
heapify(x)
nil
end
def to_a
@data
end
def self.sort(array)
heap = max(array)
heap.send(:sort)
heap.to_a
end
private
def sort
(@size - 1).times do
swap(1, @size)
@size -= 1
heapify(1)
end
end
def get(x)
@data[x - 1]
end
def set(x, val)
@data[x - 1] = val
end
def swap(x, y)
@data[x - 1], @data[y - 1] = @data[y - 1], @data[x - 1]
end
def parent(x)
x / 2
end
def left(x)
x * 2
end
def right(x)
x * 2 + 1
end
end